OLIMPIADA MATEMÁTICA ESPAÑOLA
Fase local 2006
Viernes
20 de enero de 2006
Primera Sesión (mañana)
1.
Se da un triángulo rectángulo isósceles ABC,
con el ángulo recto en C, y los
catetos de longitud 2. Un arco de círculo l
con centro A divide al triángulo en
dos partes de la misma área, mientras que el arco de círculo m con centro en B es tangente al arco l en un punto de la hipotenusa AB.
Hallar el área de la porción del triángulo no cubierta por los sectores circulares correspondientes a los dos arcos.
2.
Se suponen conocidas las raíces reales de las n ecuaciones de segundo grado que se indican en el siguiente
cuadro:
|
Ecuación |
Raíces |
|
|
|
|
|
|
|
|
|
|
|
|
Encontrar, razonadamente, las raíces de la ecuación
.
3. En
el triángulo ABC se traza la
bisectriz interior CD. Se sabe que el
centro del círculo inscrito en el triángulo BCD
coincide con el centro del círculo circunscrito del triángulo ABC. Calcular los ángulos del triángulo ABC.
Fase local 2006
Viernes
20 de enero de 2006
Segunda Sesión (tarde)
4. Encontrar,
razonadamente, dos números enteros positivos a y b, tales que
sea múltiplo de 
,
sea múltiplo de ,
sea múltiplo de ,
sea múltiplo de ,
pero 
no sea múltiplo de .
5. Un número positivo x verifica la relación
.
Demostrar que
es entero y calcular su valor.
6. Se
considera la inecuación
,
donde a es un parámetro real.
a) Discutir la inecuación según los valores de a.
b) Caracterizar los valores de a para los cuales la inecuación tiene exactamente DOS soluciones enteras.
Fase local 2006
Viernes
20 de enero de 2006
Primera Sesión (tarde)
1. En
el sótano del castillo, 7 gnomos guardan su tesoro. El tesoro está detrás de 12
puertas, cada una de ellas con 12 cerraduras. Todas las cerraduras son
distintas. Cada gnomo tiene llaves para
algunas de las cerraduras. Tres gnomos cualesquiera tienen conjuntamente llaves
para todas las cerraduras. Probar que entre todos los gnomos tienen por lo
menos 336 llaves.
2. Determinar
todos los enteros n tales que
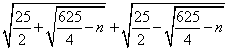
es entero.
3.
Dos esferas de radio r son tangentes exteriores. Tres esferas de radio R son
tangentes exteriores entre sí, cada una tangente a las otras dos. Cada una de
estas esferas es, además, tangente exterior a las dos primeras.
Encontrar la relación existente entre R y r.
Fase local 2006
Sábado
20 de enero de 2006
Segunda Sesión (mañana)
4. Calcular
los números p y q tales que las raíces de la ecuación
sean D y 1 – D, siendo D el discriminante de esa ecuación de segundo grado.
5. Los
números naturales 22, 23, y 24 tienen la siguiente propiedad: los exponentes de
los factores primos de su descomposición son todos impares:
.
¿Cuál es el mayor número de naturales consecutivos que pueden tener esa propiedad?. Razónese la contestación.
6.
Los vértices del cuadrilátero convexo ABCD
están situados en una circunferencia. Sus diagonales AC y BD se cortan en el
punto E. Sea 
el centro del círculo inscrito en el triángulo
ABC, y 
el centro del círculo inscrito en el triángulo
ABD. La recta 
corta a EB
en M y a EA en N.
Demostrar que el triángulo EMN es isósceles.
Fase local 2006
Sábado
20 de enero de 2006
Primera Sesión (mañana)
1. Los números
reales no nulos a y b verifican la igualdad
.
Encontrar, razonadamente, todos los valores tomados por la expresión
.
2. ¿Existe
un conjunto infinito de números naturales que NO se pueden representar en la
forma
,
siendo n natural y p primo? Razónese la contestación.
3. En
el triángulo ABC, se trazan la
bisectriz interior AL (L pertenece al lado BC), la altura BH (H pertenece al lado AC) y la mediana CM (M pertenece al lado AB).
Se sabe que los ángulos 
y 
son iguales.
Determinar, razonadamente, las medidas de los ángulos del triángulo ABC.
Fase local 2006
Sábado
20 de enero de 2006
Segunda Sesión (tarde)
4. Determinar
todas las ternas de números reales 
,
con 
,
tales que las parábolas
tienen el mismo vértice.
5. Encontrar
todas la soluciones 
reales del sistema de ecuaciones
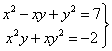
6. Decimos
que tres números naturales distintos forman una terna aditiva si la suma de los dos primeros de ellos es igual al
tercero. Hallar, razonadamente, el máximo número de ternas aditivas que puede
haber en un conjunto dado de 20 números naturales.
Soluciones en formato Microsoft Word 2000 comprimido .zip (92 Kb)
|Página principal||InfoAlumnos||InfoProfesores||Otros sitios de interés||Problemas|