Primera sesión

XXXVIII Olimpiada Matemática Española
Fase nacional 2002 (La Rioja)
Primera sesión (5 de abril)

1.- Hallar todos los polinomios P(t) de una variable, que cumplen:

P(x² - y²) = P(x + y)·P(x – y)

para todos los números reales x e y.

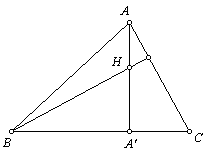
2.-En un triángulo ABC, A’ es el pie de la altura relativa al vértice A y H el ortocentro.

a)Dado un número real positivo k tal que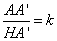

, encontrar la relación entre los ángulos B y C en función de k.

b) Si B y C son fijos, hallar el lugar geométrico del vértice A para cada valor de k.

3.-La función g se define sobre los números naturales y satisface las condiciones:

·g(2) = 1

·g(2n) = g(n)

·g(2n + 1) = g(2n) + 1

Sea n un número natural tal que 1 £ n £ 2002. Calcula el valor máximo M de g(n). Calcula también cuántos valores de n satisfacen g(n) = M.

Segunda sesión (6 de abril)

4.-Sea n un número natural y m el que resulta al escribir en orden inverso las cifras de n. Determinar, si existen, los números de tres cifras que cumplen 2m + S = n, siendo S la suma de las cifras de n.

5.-Se consideran 2002 segmentos en el plano tales que la suma de sus longitudes es la unidad. Probar que existe una recta r tal que la suma de las longitudes de las proyecciones de los 2002 segmentos dados sobre r es menor que

6.-En un polígono regular H de 6n + 1 lados (n entero positivo), R vértices se pintan de rojo y el resto de azul. Demostrar que el número de triángulos isósceles que tienen sus tres vértices del mismo color no depende del modo de distribuir los colores en los vértices de H.

No está permitido el uso de calculadoras.
Cada problema se puntúa sobre 7 puntos.
El tiempo de cada sesión es de 3,5 horas.

Soluciones en formato Microsoft Word 2000 (Comprimido .zip, 42 Kb)

Ganadores de la Olimpiada

Medallas de oro

Daniel Rodrigo López
Luis Hernández Corbato
Sergio Millán López
David García Soriano
Susana Ladra González
José Miguel Manzano Prego

Medallas de plata

Ignasi Abío Roig
Javier Cóppola Rodríguez
Víctor González Alonso
Carlos Barragán del Rey
Javier Lucas Rodríguez
Antonio Campos Domínguez
Antonio Sánchez Puente
Javier Gómez Serrano
Juan Botías Agea
Sergio José Sanabria Martín
Patricia Ceballos Carrascosa
Carlos Ruiz Mora

Medallas de bronce

Albert Llorens Martínez
Mohamed Blanca Ruiz
Eduardo Conde Pena
Alberto Fernández Pérez
Pablo Díez Renedo
Adrián Fernández Prieto
Elsa de Alfonso Prieto-Puga
Manuel López Jorge
David Morales Hidalgo
Carlos Moraga Ferrandis
Francisco Javier Pérez Grau
Gabriel García Ocejo
Alfonso Hernanz Lázaro
Gabriel González Zamudio
Mikel Arizaleta dels Horts
Jerónimo Rabaza Giner
Víctor Galilea Ruiz
José Héctor García Sánchez

Breve estudio de los resultados

Los problemas se calificaron sobre 7 puntos, Las medias y desviaciones de cada problema fueron:

	P1	P2	P3	P4	P5	P6
Medias	0,94	1,23	3,29	3,75	0,5	0,18
Desviaciones	1,736	1,780	2,401	2,547	0,843	0,465