 OLIMPIADA
MATEMÁTICA ESPAÑOLA
OLIMPIADA
MATEMÁTICA ESPAÑOLA
XXXV Olimpiada Matemática Española
Fase nacional 1999 (Granada)
Primera sesión
 OLIMPIADA
MATEMÁTICA ESPAÑOLA
OLIMPIADA
MATEMÁTICA ESPAÑOLA
XXXV Olimpiada Matemática Española
Fase nacional 1999 (Granada)
Primera sesión
![]() 1.- Las rectas t y
t’, tangentes a la parábola de ecuación y = x2
en los puntos A y B, se cortan en el punto C.
1.- Las rectas t y
t’, tangentes a la parábola de ecuación y = x2
en los puntos A y B, se cortan en el punto C.
La mediana del triángulo ![]() ABC
correspondiente al vértice C tiene longitud m.
ABC
correspondiente al vértice C tiene longitud m.
Determinar el área del triángulo ![]() ABC
en función de m.
ABC
en función de m.
![]() 2.- Probar que existe
una sucesión de enteros positivos a1, a2,…,
an, … tal que
2.- Probar que existe
una sucesión de enteros positivos a1, a2,…,
an, … tal que
es un cuadrado perfecto para todo entero positivo n.
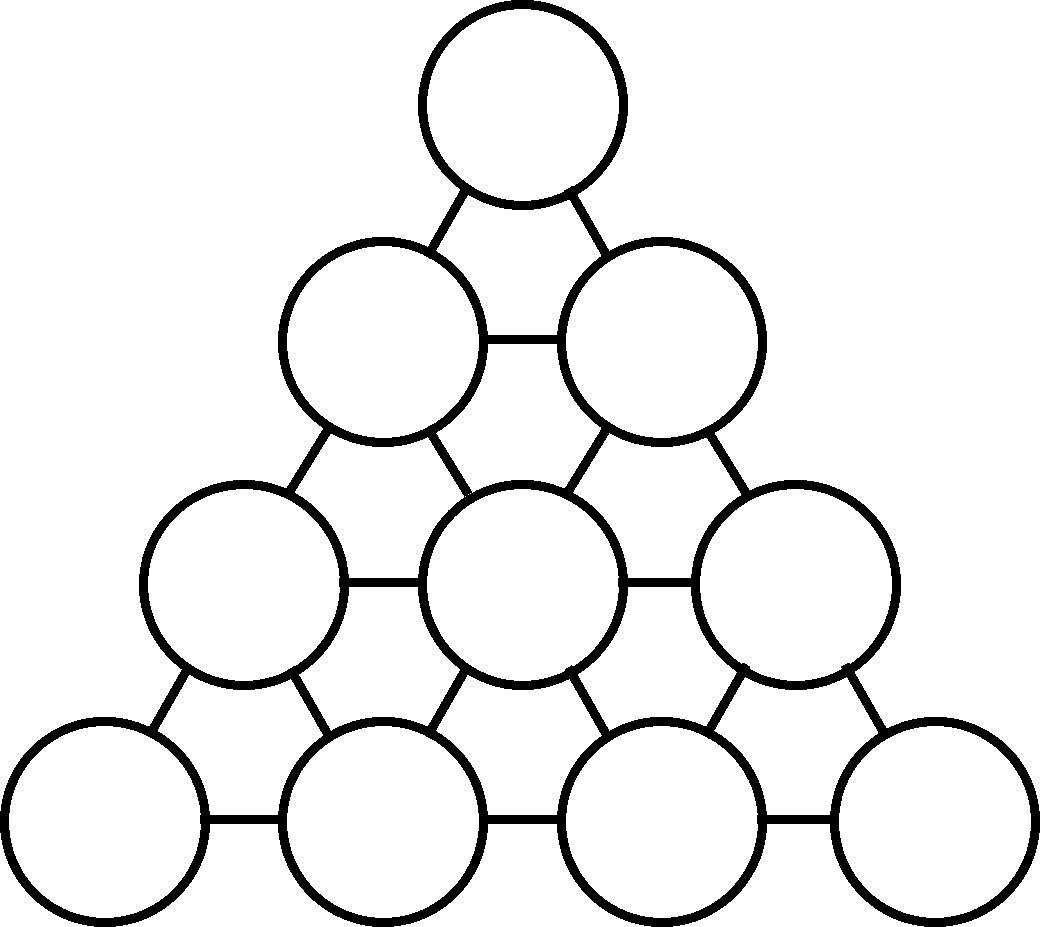
![]() 3.- Sobre un tablero
en forma de triángulo equilátero como se indica en la figura;
se juega un solitario.
3.- Sobre un tablero
en forma de triángulo equilátero como se indica en la figura;
se juega un solitario.
Sobre cada casilla se coloca una ficha. Cada ficha es blanca por un
lado, y negra por el otro. Inicialmente, sólo una ficha, que está
situada en un vértice, tiene la cara negra hacia arriba; el resto
de las fichas tiene la cara blanca hacia arriba. En cada movimiento se
retira sólo una ficha negra del tablero y se da la vuelta a cada
una de las fichas que ocupan una casilla vecina. Casillas vecinas
son las que están unidas por un segmento.
Después de varios movimientos ¿será posible quitar
todas las fichas del tablero?
Segunda sesión
![]() 4.-. Una caja contiene
900 tarjetas, numeradas del 100 al 999. Se sacan al azar (sin reposición)
tarjetas de la caja y se anota la suma de los dígitos de cada tarjeta
extraída. ¿Cuál es la menor cantidad de tarjetas que
se deben sacar, para garantizar que al menos tres de esas sumas sean iguales?
4.-. Una caja contiene
900 tarjetas, numeradas del 100 al 999. Se sacan al azar (sin reposición)
tarjetas de la caja y se anota la suma de los dígitos de cada tarjeta
extraída. ¿Cuál es la menor cantidad de tarjetas que
se deben sacar, para garantizar que al menos tres de esas sumas sean iguales?
![]() 5.- El baricentro del
triángulo
5.- El baricentro del
triángulo ![]() ABC es
G. Denotamos por
ABC es
G. Denotamos por ![]() las distancias
desde G a los lados a, b y c respectivamente.
las distancias
desde G a los lados a, b y c respectivamente.
Sea ![]() el radio de la circunferencia
inscrita. Probar que
el radio de la circunferencia
inscrita. Probar que
:i) ![]()
ii) ![]()
![]() 6.- Se divide el plano
en un número finito de regiones N mediante tres familias de rectas
paralelas. No hay tres rectas que pasen por un mismo punto.
6.- Se divide el plano
en un número finito de regiones N mediante tres familias de rectas
paralelas. No hay tres rectas que pasen por un mismo punto.
¿Cuál es el mínimo número de rectas necesarias
para que N>1999?
No está permitido el uso de calculadoras.
Cada problema se puntúa sobre 7 puntos.
El tiempo para esta sesión es de 4 horas.
Los problemas se calificaron sobre 7 puntos, Las medias y desviaciones de cada problema fueron:
|
|
|
|
|
|
|
|
| Medias |
2,44
|
1,09
|
1,91
|
4,86
|
0,52
|
1,52
|
| Desviaciones |
2,648
|
2,067
|
2,155
|
2,85
|
1,242
|
2,151
|
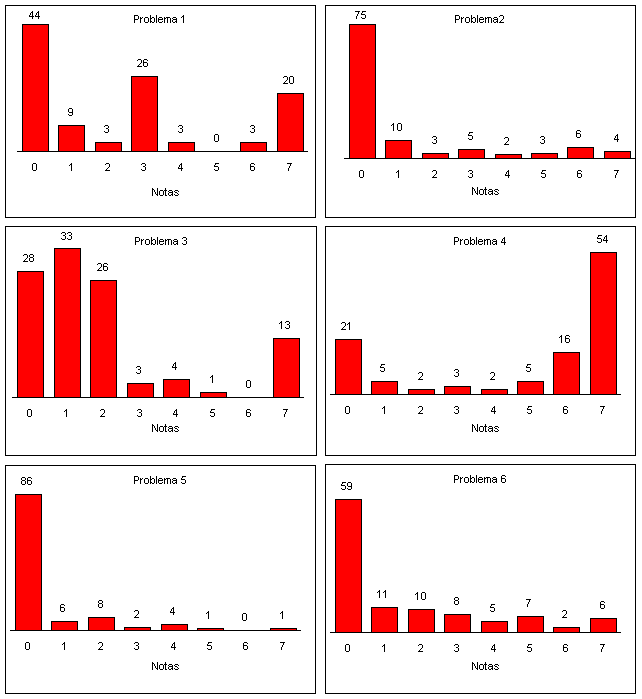
El gráfico siguiente muestra las frecuencias de notas para cada
problema.
|Página principal| |Info
Alumnos| |Info Profesores| |Otros
sitios de interés| |Problemas|
Copyright © C. Sánchez-Rubio
Actualizado 22 Marzo 1999